அடுத்துள்ள
இரு உறுப்புகளுக்கு இடையேயுள்ள வித்தியாசம் சமனாகவுள்ள எண் தொடர்கள் கூட்டல் விருத்தி எனப்படும்.
உதாரணம்
-01
இக்
கூட்டல் விருத்தியானது குறிப்பிட்ட எண்வரை தொடரும்…
அடுத்து
நாம் கூட்டல்
விருத்தி ஒன்றின்
n வது உறுப்பைக்
காண்போம்
உறுப்பு விபரம்
|
கூட்டல் முறை
|
பெருக்கல் முறை
|
குறியீட்டு முறை
|
1 வது உறுப்பு
|
3
|
3 + 4(0)
|
3 + 4(1-1)
|
2 வது உறுப்பு
|
3+4
|
3 + 4(1)
|
3 + 4(2-1)
|
3 வது உறுப்பு
|
3+4+4
|
3 + 4(2)
|
3 + 4(3-1)
|
4 வது உறுப்பு
|
3+4+4+4
|
3 + 4(3)
|
3 + 4(4-1)
|
5 வது உறுப்பு
|
3+4+4+4+4
|
3 + 4(4)
|
3 + 4(5-1)
|
...
... ...
|
|||
100 வது உறுப்பு
|
3+ 4 (99)
|
3 + 4(99)
|
3 + 4(100-1)
|
இதை
பின்வருமாறு குறித்துக் காட்டலாம்….
இங்கு
a = முதலுறுப்பு , d = பொது வித்தியாசம்
உறுப்பு விபரம்
|
கூட்டல் முறை
|
பெருக்கல் முறை
|
குறியீட்டு முறை
|
1 வது உறுப்பு
|
a
|
a + d(0)
|
a + d(1-1)
|
2 வது உறுப்பு
|
a+d
|
a + d(1)
|
a + d(2-1)
|
3 வது உறுப்பு
|
a+2d
|
a + d(2)
|
a + d(3-1)
|
4 வது உறுப்பு
|
a+3d
|
a + d(3)
|
a + d(4-1)
|
5 வது உறுப்பு
|
a+4d
|
a + d(4)
|
a + d(5-1)
|
...
... ...
|
|||
100 வது உறுப்பு
|
a+ 99d
|
a + d(99)
|
a + d(100-1)
|
n வது உறுப்பு
|
a+ (n-1) d
|
a + d(n-1)
|
a + d(n-1)
|
எனவே
கூட்டல் விருத்தியின் n வது உறுப்பை காண்பதற்கான சமன்பாடு…
கூட்டல் இடை
இரு
எண்களிற்கு நடுவில் வரும் உறுப்பு கூட்டல் இடை எனப்படும்.
a,b,c
என்பன கூட்டல் விருத்தி ஒன்றின் அடுத்துள்ள 3 உறுப்புகள் ஆயின்
b இன் பெறுமதியானது , a,b ஐ சேர்த்து வரும் பெறுமதியின் அரை மடங்காக இருக்கும்.
அடுத்து
நாம்…..
கூட்டல் விருத்தி
ஒன்றின் கூட்டுத்
தொகையைக் காண்போம்..
கூட்டல்
விருத்தி ஒன்றின் கூட்டுத்தொகையை காண்பதற்கு சாதாரண சமன்பாடு ஒன்றை கொண்டு கணிக்கலாம், அச் சமன்பாடு எவ்வாறு பெறப்பட்டது எனப் பார்ப்போம்.
ஒரு
தொடர் பின்வருமாறு அமையிம்.
S = a +
(a + d) + ... + (a + (n-2)d)
+ (a +
(n-1)d)
இதை முரணாக எழுதுவோம்….
S = (a + (n-1)d) + (a + (n-2)d) + ... + (a + d) + a
இனி
இவ் இரண்டையும் கூட்டினால்…
2S = n × (2a + (n-1)d)
அல்லது
:



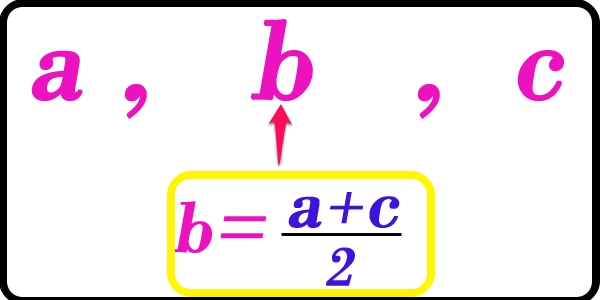



No comments:
Post a Comment